在上一篇為什麼圖地反轉的設計具有魔法?你也可以是圖地反轉魔術設計人中文章講到圖地反轉的魔力，一個魔術技法當然不能限於一種，這會很枯燥。
那麼，這個新的魔術技法相較於圖地反轉還要更加精彩、更加有智慧—矛盾圖型，也就是說矛盾圖型是圖地反轉的延伸。
矛盾圖形運用空間成立，但卻沒辦法在現實生活中成立，換句話說，它的存在於平面以及影音方面，所以矛盾圖形操弄人的心理狀態，產生這樣到那樣會不能成立，可是又會覺得合理又詭異心理。
內容目錄
矛盾圖形的意義?
矛盾圖型有人稱它為悖理圖形或者不可能的圖形，一般來說，在二次元畫面上存在矛盾圖型這是合理，可是卻又不能在現實上出現，所以儘管出現這種衝突，它還是一樣依然在二次元發生。
關於矛盾圖型的意義在哪?我認為既然存在二次元又還沒到三次元的視覺魔術，觀者可以肯定在三維以及四維的發生，那麼其實要說的話，若要追求視覺變化，我們不能用單一角度去看事情。
邊洛斯三角形
這是一個相當特殊有名的矛盾圖形中的三角形，主要以三個長方形下去組成，他們的三個角邊長夾角都是直角，但是奇怪的點是，一般我們都知道三角形的的所有夾角總和等於180度，可是，邊洛斯三角形卻不成立。
一名英國數學物理學家羅傑·潘洛斯（Roger Penrose，1931年至今）與他的父親共同設計這種三角形，所以又有人稱潘洛斯三角形（Penrose Triangle）。
這種三角形的研究與設計後來就被他跟他父親一同推廣，1958年在《英國心理學月刊》（British Journal of Psychology）中發表。
三角矛盾圖形竟然在生活上成立?
我們在前面講到說矛盾圖形不可能存在生活上，單純生在平面中發生，沒想到竟可以活生生出現在眼前?!
澳大利亞的西部大城市東柏斯克萊斯布洛克廣場（Claisebrook Square）就一個超大型裝置藝術，這種裝置目測大約有四層樓高度，看起來不可能辦到的三角形到底怎麼創造邊洛斯三角形?
這是澳洲的東柏斯改造計畫之一，找來一名藝術家布萊恩麥凱（Brian McKay）與一名建築師艾哈邁德阿巴斯（Ahmad Abas）等人共同製作騙人的「魔術手法」。
這個魔術手法是他走到一個特定位置會呈現邊洛斯三角形，而如果離開了原本的角度則是另一個純粹藝術而已，不管怎麼看都還是一樣沒有三角形。
接著，我們飛到另一個國家，比利時歐波芬村莊(Kingdom of Belgium, Ophoven)。
在這個村莊裡面有一個地景也有用到邊洛斯三角形，同樣的運用「魔術」，到特定角度去觀看才能發現有三角形，只不過它不像澳洲一樣有斷開，而是在另一個角度會發現有緞帶曲折樣子。
我們都知道美國2010年上映科幻電影《全面啟動》(Inception)中有一幕運用到矛盾圖形中的不可能的階梯，這個階梯其實也是並非真實存在，它也是需要透過另一種角度觀看。
美國私立羅切斯特大學(University of Rochester，UR)，就有放出一個相當有趣的影片，一個人在樓梯間走上去後照理說應該是往上走，畫面上的先生竟然從下面走上來。
提外話：無限循環帶
我們都知道圖的反轉的天才是艾薛爾(Maurits Cornelis Escher，1898年-1972年)，但是運用矛盾圖形的藝術家也是艾薛爾，除了使用邊洛斯三角形概念以外，還與該三角形的相似手法—莫比烏斯帶。
莫比烏斯帶(Möbius strip)有人稱它為莫比烏斯環、梅比斯帶、麥比烏斯帶等相似之義，這主要由德國天文學家、數學家莫比烏斯(August Ferdinand Möbius，1790年-1868年)以及另一個德國數學家約翰．李斯丁在1858年發現此特殊性質，便以莫比烏斯取名為莫比烏斯環。
那麼這個環，也是在位相幾何學占重要一環，主要是一條直線在它的尾端捲一下，並連接前端的頭，也就是說即使走到終點也會走到其點的開始，它就形成了一個無限循環的迴圈。
早期力學家也在困擾這件事，想要以方程式試圖解開，接著英國兩名科學家就破解莫比烏斯環謎團，最後的答案的解釋與能量密度有關。
艾薛爾為此有了靈感，運用莫比烏斯環裡，上面有著幾隻小螞蟻，在這樣的視覺上無限循環又更加真實，所以也是莫比烏斯環二代。
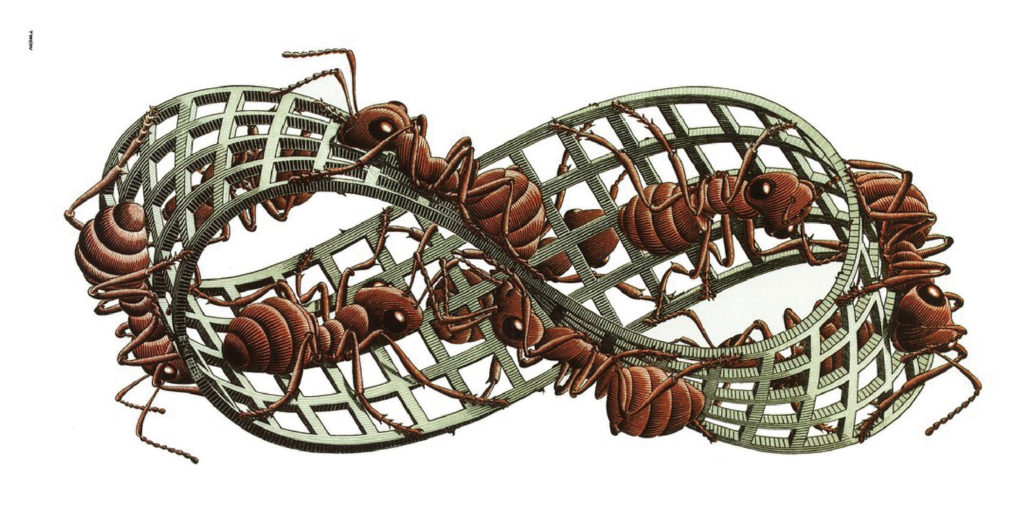
以民間來說，卻認為是一種詛咒，一旦掉入迴圈中，就出不來。
韓國導演金基德作品《莫比烏斯》，它主要也是訴說家庭倫理恐怖的故事。
以神話來說，有一個與莫比烏斯環相似的符號，銜尾蛇(Ouroboros，又叫咬尾蛇)是一條龍或蛇的樣貌，牠咬著尾巴，象徵自我吞食、無限大以及循環等意思，另一個知名心理學家榮格的觀點，卻認為是只是純粹反映人類心理而已。
矛盾圖形製作：邊洛斯三角形
Step1.首先打開設計軟體Adobe illustrator，製作一個三角形，漸層一下。
Step2.往下複製一個三角形，並且交疊，在裁減部分剩餘。
Step3.接著，正的必須左右切60度的相同角度，然後各個在大方向轉移60度，拼湊起來之後，再按上排的視窗底下路徑管理員，出現小框框，按分割並右鍵解散群組，之後就能發現移位多餘的刪除。
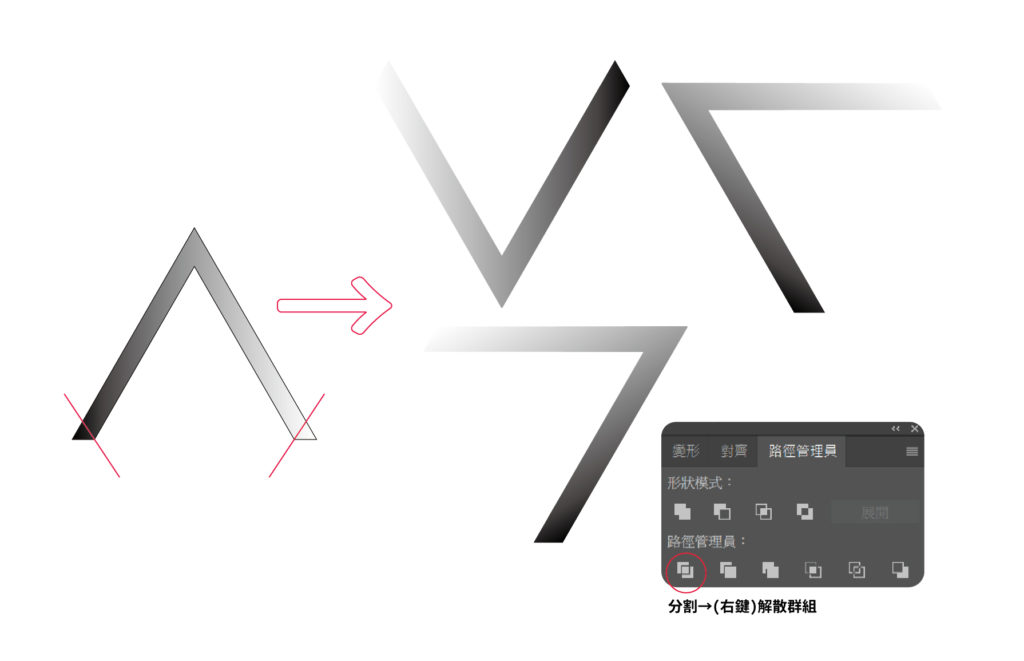
Step4.接著矛盾圖形的三角形就完成了。
你可能會喜歡的文章….
■國際設計比賽有哪些?你也可以設計人更是厲害的設計強者！
■點線面思考很重要?讓我告訴你德國包浩斯設計學校教的點線面
■第一次世界大戰後成立設計界的經典:德國包浩斯設計學校
■視覺元素是什麼?設計人創造視覺元素的秘密報給你知！
■什麼是錯視?運用視覺設計的錯視去欺騙別人，甚至還心甘情願的被騙
■圖文設計編排是什麼?7種創造強而有力的圖文設計旁白
每次看到這種圖形的時候，都超驚訝的！
很想嘗試去那個樓梯走走看
哈哈哈那只能在視覺上走了喔
這個好酷喔！在一般的概念裡是不能成立的但是確實成立了，思想上的矛盾，覺得版主舉的例子都很貼切呢！還有名稱的緣由，真的很專業
哇靠這三角形我知道！想不到版主會介紹的這麼深入
謝謝拉XDDD